Is the Time It Takes for a Light Bulb to Burn Out Discrete or​ Continuous
Distributions of Data
Part 1.2: Expected Lifetime
Now we return to the question of the expected life of a bulb. Suppose that all we know about the burnout times of the bulbs is the function F. How can we use that information to define and calculate an average lifetime?This is a challenging problem for two reasons. First, lifetime is not a discrete quantity: A bulb can burn out at any instant over a long continuous time interval. Second, the time interval is unbounded. In principle, an exceptional light bulb could burn "forever" or at least for a very long time relative to the usual lifetimes of light bulbs.
We start by considering a discrete approximation to our continuous problem that does not have these two drawbacks. The first examples we'll consider won't model our real light bulbs very well. However, these calculations will show us how to deal with the real situation.
- Suppose we have a collection of (idealized) bulbs, all mixed up in one box, of exactly two types:
- Type A burns out in exactly 35 days, and we have 50 of these.
- Type B burns out in exactly 63 days, and we have 100 of these.
- Suppose now that we have a collection of three types of bulbs, each with an exact lifetime and a probability of occurrence given in table below. What is the expected life of a bulb drawn at random from this collection?
Type Probability Exact lifetime 1 p1 = 1/4 t1 = 23 days 2 p2 = 1/2 t2 = 47 days 3 p3 = 1/4 t3 = 65 days - If we have n types of bulbs, the kth occurring with probability pk and having a lifetime of exactly tk , for k = 1, 2, ..., n, explain why the expected life of a bulb taken at random from this collection should be
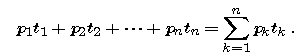
- Calculate F(200).
Now we develop an integral to calculate the average lifetime. We choose a large integer n, and we imagine the time interval from 0 to 200 divided into n subintervals, each of length ![]() t = 200/n. Our real bulbs don't have exact lifetimes, of course, but we will approximate the expected lifetime by pretending that they do: If a bulb burns out between the time tk-1 = (k - 1)
t = 200/n. Our real bulbs don't have exact lifetimes, of course, but we will approximate the expected lifetime by pretending that they do: If a bulb burns out between the time tk-1 = (k - 1)![]() t and the time tk = k
t and the time tk = k![]() t, then we will count it as having burned for exactly tk days. We are now in the situation described by the expression
t, then we will count it as having burned for exactly tk days. We are now in the situation described by the expression
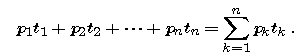
Here pk = F(tk) - F(tk - 1) for k = 1, 2, ... n. We can thus approximate the expected lifetime of a random bulb by the sum

This sum does not look quite like an approximating sum for an integral -- it is lacking a factor of ![]() t in each term. Our solution to this problem is to multiply and divide each term of the sum by
t in each term. Our solution to this problem is to multiply and divide each term of the sum by ![]() t, which does not disturb the value of the sum. Then we factor
t, which does not disturb the value of the sum. Then we factor ![]() t out of each term, which permits us to write the sum in the form
t out of each term, which permits us to write the sum in the form

For large values of n, ![]() t is small, and
t is small, and

(The difference quotient is also approximately F'(tk-1). When tk and tk-1 are very close together, the corresponding values of F' also will be very close together.) If we abbreviate the derivative of F by f, then our approximate expression for the expected lifetime becomes

As n gets large, this sum approaches the integral

Now the only reason we selected 200 as the upper limit for our integral is that, in the present context, 200 is "big." However, any bigger upper limit b would work as well -- indeed, better. So we really should define the expected life of a random bulb to be

that is,
 .
.- Assuming r = 0.032, determine the function f. Then find the corresponding expected life of a bulb.
Source: https://services.math.duke.edu/education/postcalc/data/data1_2.html
0 Response to "Is the Time It Takes for a Light Bulb to Burn Out Discrete or​ Continuous"
Enregistrer un commentaire